doi: 10.58763/rc2023117
Scientific and Technological Research Article
Design and implementation of a game-based activity to promote learning of game theory
Diseño e implementación de un ejercicio lúdico para promover el aprendizaje de la teoría de juegos
Carlos
Felipe Ardila Otero1 ![]() *, Lissette Vanessa Pérez
Rueda1
*, Lissette Vanessa Pérez
Rueda1 ![]() *,
Marí Camila Ballesteros Peña1
*,
Marí Camila Ballesteros Peña1 ![]() *, Martha Liliana
Torres-Barreto1
*, Martha Liliana
Torres-Barreto1 ![]() *
*
ABSTRACT
Game theory, an interdisciplinary field that explores interactions among entities in strategic scenarios, is paramount for understanding how individuals make decisions in interactive situations. This paper outlines the development and evaluation of a playful exercise to facilitate understanding fundamental concepts such as dominant and dominated strategies and Nash equilibrium, employing a 'design thinking' methodology. An empirical evaluation was conducted with 76 Industrial Engineering students from the Universidad Industrial de Santander, dividing them into four teams representing companies vying for customers. The teams assessed payoff matrices and made marketing decisions, utilizing a colored die to eliminate non-advantageous strategies. Findings indicate a significant increase in interest in game theory, with 86% of participants expressing a preference for this method compared to conventional classes. Furthermore, 81% desired to incorporate this activity into their regular courses, while 76% applied previous knowledge during the training. An average improvement of 17% in correct responses suggests that the playful exercise effectively facilitates the assimilation of key concepts in game theory among university students. This study underscores the potential of integrating active activities based on game theory to enrich the learning process in an academic context.
Keywords: playful activity, design thinking, Nash equilibrium, dominant and dominated strategies, game theory.
JEL classification: I20, I21
RESUMEN
La teoría de juegos, un campo interdisciplinario que explora las interacciones entre entidades en escenarios estratégicos, es esencial para entender cómo los individuos toman decisiones en situaciones interactivas. Este artículo describe el desarrollo y evaluación de un ejercicio lúdico orientado a facilitar la comprensión de conceptos fundamentales como estrategias dominantes y dominadas, y equilibrio de Nash, utilizando la metodología 'design thinking'. Se llevó a cabo una evaluación empírica con 76 estudiantes de Ingeniería Industrial de la Universidad Industrial de Santander, dividiéndolos en cuatro equipos que representaban empresas en competencia por clientes. Los equipos evaluaron matrices de pagos y tomaron decisiones de marketing, utilizando un dado de colores para eliminar estrategias no ventajosas. Los hallazgos indican un incremento significativo en el interés por la teoría de juegos, con un 86% de los participantes expresando una preferencia por este método en comparación con las clases convencionales. Además, el 81% manifestó su deseo de incorporar esta actividad en sus cursos regulares, mientras que el 76% aplicó conocimientos previos durante la actividad. Un aumento promedio del 17% en las respuestas correctas sugiere que el ejercicio lúdico efectivamente facilita la absorción de conceptos claves en la teoría de juegos por parte de los estudiantes universitarios. Este estudio subraya el potencial de integrar actividades lúdicas basadas en la teoría de juegos para enriquecer el proceso de aprendizaje en el contexto académico
Palabras clave: actividad lúdica, design thinking, equilibrio de Nash, estrategias dominantes y dominadas, teoría de juegos.
Clasificación JEL: I20, I21
Received: 18-04-2023 Revised: 05-06-2023 Accepted: 15-06-2023 Published: 04-07-2023
Editor: Carlos Alberto Gómez Cano ![]()
1Universidad Industrial de Santander. Bucaramanga, Colombia
Cite as: Ardila, C., Pérez, L., Ballesteros, M. y Torres-Barreto, M. (2023). Diseño e implementación de un ejercicio lúdico para promover el aprendizaje de la teoría de juegos. Región Científica, 2(2), 2023117. https://doi.org/10.58763/rc2023117
INTRODUCTION
Game theory has proven to be applicable in many business domains and has been the subject of study by numerous authors and experts in the field (Ahmad et al., 2023; Hallinger & Wang, 2020; Mehmanpazir et al., 2022). Game theory is valuable for modeling situations with multiple players and interdependent decisions (Ahmad et al., 2023; Nash & John, 1950). This tool can be used in business to analyze and solve complex problems related to strategy, negotiation, collaboration, and decision-making (Tasnim et al., 2023). In particular, game theory has been successfully used in areas such as industrial economics (Mohamed et al., 2019), human resource management (Hafezalkotob et al., 2023), and business strategy (Jain et al., 2020; Ozkan-Canbolat et al., 2016).
Game theory provides a theoretical framework and tools for analyzing complex business situations and making strategic decisions (Rzeczycki, 2022). It is a versatile and applicable discipline that has proven helpful in many aspects of the business world (Cullen et al., 2022). It is a branch of mathematics used to model and analyze situations where two or more parties interact and have conflicting objectives (Sun et al., 2021; Vanda et al., 2022). An important concept in game theory is that of zero-sum games (Wang et al., 2023; Wu & Lisser, 2023). A zero-sum game is one in which the success of one party depends on the failure of the other (Wu & Lisser, 2022). For example, a pricing situation in which two companies compete for the same market is an example of a zero-sum game.
Another relevant concept is dominant and dominated strategies (Valle, 2019). A dominant strategy is the best option for a player regardless of the actions of others (Amorós, 2022). On the other hand, a dominant strategy is worse than other options for a player regardless of the actions of others (Loertscher & Marx, 2020).
Understanding these concepts can be helpful for companies when making strategic decisions, as it allows them to anticipate the response of their competitors and optimize their actions. Some studies have demonstrated the effectiveness of game theory in predicting business behavior and identifying opportunities for collaboration and competition (Bonsón et al., 2023).
Game theory and its concepts, such as zero-sum games and dominant and dominated strategies, can be a valuable tool for companies to make strategic decisions and to understand the dynamics of competition and collaboration in their industry. Nash equilibrium is one of the most important concepts within game theory and is widely used to analyze the interaction between competitors in a market (Hou et al., 2020; Zeng et al., 2023). According to Nash and John (1950), a Nash equilibrium is a combination of strategies in which no player can improve their position by choosing a different strategy. In other words, it is a point at which the players have found the best strategy given the behavior of the other players. This applies in business, for example, in pricing, where a firm must consider the strategy of its competitors when determining its strategy (Do, 2022; Liu, 2021).
On the other hand, gamification is increasingly being used in educational (Seymour et al., 2023) and business environments (Cechella et al., 2021). This technique involves applying game elements and dynamics in contexts unrelated to leisure to improve students' or employees' motivation, loyalty, and cooperation (Suárez-López et al., 2023). Gamification has been identified as an innovative methodology that transforms social and cultural relationships and contributes to positive individual, occupational, economic, and social changes.
The topic of gamification has been addressed by several authors, among them the work of Munhoz (2020), who has classified the elements of gamification, in correspondence with Werbach and Hunter, into three categories: dynamics, mechanics, and components. Another critical study is that of Deterding et al. (2011), who have delved into the importance of motivation in gamification and pointed out how this technique has become increasingly popular for improving motivation and learning. Gamification is a technique that has been increasingly used in recent years to motivate users to adopt certain behaviors. Applying gamification elements to different contexts, including work and education, effectively improves motivation and engagement (Deterding et al., 2011).
It is essential to understand the different types of players in gamification, as this can influence how games are designed and how players experience and respond to them. According to Richard Bartle's theory, there are four types of players in games: adventurers, crafters, maquis, and social players (Bartle, 1996). Adventurers enjoy exploration and overcoming challenges, while crafters enjoy creating and building. Maquis enjoy conflict and competition, and socials enjoy interacting and building relationships with other players.
These four types of players can be relevant for companies implementing gamification, as it is essential to understand player preferences and motivations to design practical and appealing games. For example, a company that wants to motivate its employees to adopt more sustainable behaviors could design a game that appeals to adventurous and crafty gamers who enjoy exploration and creation. At the same time, it could also include elements of competition and socialization to appeal to maquis and social gamers. Understanding the different types of gamers in gamification is essential for companies that want to implement effective and engaging games for their employees and customers.
In this sense, creating a gamification activity that addresses the topic of dominant and dominated strategies and Nash equilibrium is an excellent way to help students understand these concepts more simply and enjoyably. Therefore, in this article, we describe the process of creating a playful activity on these topics and the validation of its effectiveness through an evaluation with students.
METHODS
Design Thinking is a human-centered problem-solving methodology Murphy proposed (Murphy, 2016). Its main objective is to understand people's needs and challenges and generate innovative and effective solutions. This methodology comprises five main phases: understanding, definition, ideation, prototyping, and evaluation. In this project, these phases have been tailored to specific needs, and the process was developed following a set of customized phases:
1. Selection of the topic: An analysis was made to identify the specific area within operations research on which the company wished to work to obtain optimal results.
2. Analysis of the environment: An investigation was carried out to determine which group of people would be the target, that is, which users would benefit from creating the recreational activity.
3. Background analysis: A thorough review of available information on past operations research-focused play activities was conducted to establish a point of comparison and clarify any unclear issues related to the topic.
4. Ideation of the ludic: A brainstorming session was conducted to identify the topics to be addressed in the ludic activity, followed by an evaluation of each topic.
5. Creation of the game: During this stage, the selected topics were detailed, and the structure of the play activity was defined.
6. Validation of the game: An evaluation was conducted with students to obtain feedback on the design and other features of the game activity.
Type of study
This study focused on describing reality and providing an interpretation of it, so it has a descriptive approach (Sabino, 2014). In addition, it used a non-experimental design that involves analyzing the results of a validation process without intervening in the variables.
Instrument
A previously validated survey was adapted to evaluate the play activity (Reyes et al., 2020). The survey was developed in Google Forms and consists of 15 questions, where 10 of them were evaluated using a 5-point Likert scale, with 1 indicating total disagreement and 5 indicating total agreement. Two questions were multiple choice, and two were open-ended, allowing respondents to express themselves freely. In addition, further assessments of prior knowledge and learning were conducted to determine whether the play activity met its objective of helping students understand the concepts of dominant and dominated strategies more simply and enjoyably, as well as Nash equilibrium.
Population and sample
In the validation process, we worked with a population of 76 students selected using a non-probabilistic convenience sampling. From the total population, a sample of 16 students belonging to two different groups of the same University in Industrial de Santander (Colombia) was obtained, specifically from the Introduction to Industrial Engineering and Operations Research courses. The previously designed and validated survey was applied to this sample.
Phase 1. Topic selection
A thorough analysis of possible areas for the development of the ludic activity was carried out, considering three factors: (1) the difficulties that advanced students experienced when learning specific topics of their career subjects; (2) four meetings with three Industrial Engineering students, in which topics that they would like to be included in the ludic activity were identified; and (3) a review of the existing ludic activities in the Educational Innovation Laboratory GALEA of the Universidad Industrial de Santander, in order to know the areas in which a ludic activity was needed. Based on these factors, it was concluded that creating a game activity focused on game theory, a topic part of the Operations Research syllabus, was necessary.
Phase 2. Analysis of the environment
The target population for game development was defined in this project phase. An exhaustive review of the curriculum of the Schools of Industrial and Business Studies (EEIE) and Economics and Administration was carried out in order to identify the subjects that include topics related to game theory in their teaching plans, such as Introduction to Industrial Engineering, Operations Research II and Microeconomics II. Figure 1 presents the average number of students enrolled in each subject. The final objective is to implement the game activity in a group of 26 Industrial Engineering students.
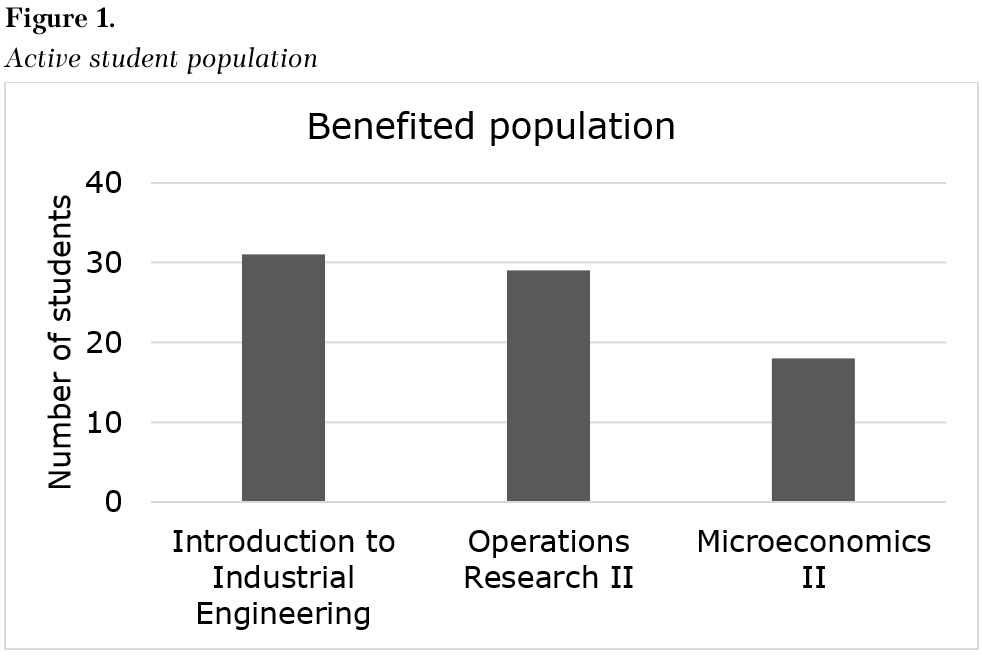
Source: own elaboration.
Phase 3. Background analysis
A bibliographic review of articles related to operations research and a search within the portfolio of gamified games and exercises offered by the Educational Innovation Laboratory of the Universidad Industrial de Santander, GALEA, where it was evidenced that there are several gamified activities in this area, such as Inventory Shoes, Optimization Laboratory, Hungarian Casino and Optimization Consultants. Likewise, previous studies on playful activities in game theory were not found. Despite this, several cases of success in the application of participatory and dynamic strategies in game theory learning were identified, as presented in table 1.
|
Table 1. Success stories |
||
|
Author (year) |
Name |
Description |
|
(Tarifa et al., 2011) |
Game theory applied to public policies. Case study: public goods. |
Game theory is used to analyze the interactions between actors in a political system and to understand how these interactions can affect public policy decision-making and outcomes. The authors argue that game theory can be a valuable tool to inform public policy decision-making and improve public policy effectiveness and efficiency. They also provide a detailed analysis of how game theory can be applied to different policy contexts and present some examples of how game theory has been used to inform public policy decision-making in different parts of the world. |
|
(Shi et al., 2022) |
An auction model enhanced with Bayesian games for federated cloud services using blockchain. |
An improved auction model with Bayesian game theory for federated cloud services using blockchain technology is presented. Bayesian game theory resolves conflicts and optimizes resource allocation in a federated cloud environment. In contrast, blockchain technology ensures transparency and security in cloud resource management. The study demonstrates that the proposed model can improve the efficiency and effectiveness of resource management in a federated cloud environment. In addition, the authors also provide an empirical evaluation of the proposed model, demonstrating its feasibility and ability to improve resource management efficiency in a federated cloud environment. |
Source: own elaboration.
Additionally, the authors attended Microeconomics II classes taught at the School of Economics and Administration of the Universidad Industrial de Santander; during these classes, it was observed that the realization of activities related to game theory makes learning more effective compared to the mere explanation of the mathematical theory of the subject (Palacio & Cortés, 2020).
Phase 4. Ideation of the games
Four meetings were held with three GALEA Lab students to conduct a brainstorming session to obtain information on possible strategies for creating a playful activity. The main objective was identifying relevant topics and appropriate tools to plan and develop the activity. The brainstorming session sought to create a space to propose creative and innovative ideas and to foster exchange and collaboration to enhance imagination and divergent thinking. All ideas presented by team members were recorded on a digital board to facilitate the visualization of all options and avoid duplication.
Once an optimal amount of ideas was collected, a process of grouping and selection was carried out based on the most relevant aspects, such as activities and dynamics suitable for fulfilling the research objective. This process was repeated in the remaining remote and face-to-face meetings, resulting in significant advances that boosted the creation of the new ludic activity.
Phase 5. Creation of the game
At this stage, the prototype of the recreational exercise was developed. The ideas were materialized and gathered in a single document that included a detailed description of the dynamics, a list of necessary materials, a plan for the correct arrangement of the spaces, defined times for each stage of the exercise, and an estimate of the number of participants required. This document was used as the basis for the planning and executing the recreational activity. The activity was conceived to be carried out in a classroom, with an estimated one-and-a-half hours duration, however, this time may fluctuate depending on the participant's reactions to the proposals during the activity.
Goal. The analysis of the proposed strategies of each company to obtain the most points by eliminating the dominated strategies in the payment matrix.
Criteria or rules.
1. Once teams have been established, no member is allowed to transfer to another group.
2. The quantitative evaluation procedure is carried out by points assigned for the elimination of a dominated strategy.
3. The team with the highest number of points is declared the winner.
Plan. Initially, the explanation of the game is developed by the auxiliary group in charge; the dynamics will consist of several consecutive rounds and about four teams will be formed, each with a maximum of 8 participants. The teams will be called Company A, Company B, Company C, and Company D. The participants will be presented with a hypothetical case in which four companies manufacture a toy and compete to attract customers. The companies must simultaneously decide whether or not to engage in advertising. To illustrate this example, an introductory activity will be conducted:
Introductory Activity: In the introductory activity, it will be stated that if two companies contract advertising, both advertising campaigns will offset each other, and each company will make 3.5 million profits. If neither company engages in advertising, each company will make 8 million profit. However, if one company hires advertising and the other does not, the one that hires will make 20 million profit, and the one that does not will make 1.5 million profit. Students should create a matrix and decide whether to plan a marketing strategy for the next year to maximize profits. This step is estimated to take 10 minutes.
Taking turns, each team will roll a colored die to identify the type of activity to be performed. Each team will take a card of the color indicated on the die, and a coach will read the instructions aloud. If the team answers correctly or meets the challenge, they will win the opportunity to eliminate the strategy that least suits their company. The team that correctly selects the strategy will earn 10 points to be added to the total to determine the final winner of the game activity.
Input resources. For the correct development of the recreational activity, the payment matrix (provided by the authors), colored dice and challenge cards (provided by the authors), a video Beam, 30 chairs, and two tables are required.
Phase 6. Validation of the games
Three sessions were carried out to validate the game, two with students taking the course Introduction to Industrial Engineering and one with students taking Operations Research II. Each session had an average of 19 participants, adding up to 59 students belonging to the Industrial Engineering program of the Industrial University of Santander, where the recreational activity was implemented. At the end of the activity, a designed instrument was used and applied through the Google Forms tool; the results are summarized in table 2.
|
Table 2. Questions for validation of the game |
|
|
Questions for prototype validation |
|
|
Likert scale questions |
|
|
1 |
The game is clear and understandable. |
|
2 |
It generates my interest in game theory |
|
3 |
I use my previous knowledge in the development of the activity. |
|
4 |
I found it easy to understand the game |
|
5 |
If I had a choice, I would like to have the game once a semester in the operations research course. |
|
6 |
Find the chair completely absorbed my attention |
|
7 |
I found the way in which the answer was arrived at to be simple. |
|
8 |
It was easy for me to eliminate the dominated strategies. |
|
9 |
It was obvious what the dominant strategy was going to be |
|
10 |
I feel tired at the end of the game |
|
Multiple choice questions with only one answer |
|
|
11 |
What strategy I used for the elimination of the strategies |
|
|
|
12 |
The challenges that were made to have the opportunity to eliminate a strategy were: |
|
a. Fun b. Good c. Not very creative d. Boring |
|
|
Open question |
|
|
13 |
What do you think of the proposed matrix? If you did not like it, please indicate why you did not like it. |
|
14 |
Comments and/or suggestions |
Source: own elaboration.
From questions 1 to 14, the results presented in table 3 were obtained.
|
Table 3. Consolidated responses to the questionnaire |
||||||||||
|
Validation scale |
||||||||||
|
Ask |
Strongly disagree |
Disagree |
Neither agree not disagree |
Agreed |
Totally agree |
|||||
|
1 |
0 |
(0%) |
3 |
(5%) |
9 |
(15%) |
24 |
(41%) |
23 |
(39%) |
|
2 |
0 |
(0%) |
1 |
(2%) |
7 |
(12%) |
19 |
(32%) |
32 |
(54%) |
|
3 |
2 |
(3%) |
2 |
(3%) |
10 |
(17%) |
18 |
(31%) |
27 |
(46%) |
|
4 |
3 |
(5%) |
5 |
(8%) |
13 |
(22%) |
21 |
(36%) |
17 |
(29%) |
|
5 |
1 |
(2%) |
1 |
(2%) |
9 |
(15%) |
11 |
(19%) |
37 |
(63%) |
|
6 |
0 |
(0%) |
4 |
(7%) |
11 |
(19%) |
13 |
(22%) |
31 |
(53%) |
|
7 |
2 |
(3%) |
7 |
(12%) |
14 |
(24%) |
17 |
(29%) |
19 |
(32%) |
|
8 |
3 |
(5%) |
3 |
(5%) |
14 |
(24%) |
17 |
(29%) |
22 |
(37%) |
|
9 |
2 |
(3%) |
6 |
(10%) |
19 |
(32%) |
16 |
(27%) |
16 |
(27%) |
|
10 |
25 |
(42%) |
14 |
(24%) |
6 |
(10%) |
10 |
(17%) |
4 |
(7%) |
Source: own elaboration.
According to the results obtained from the survey, 80% of the participants who validated the game activity considered that it was straightforward to understand. In comparison, 64% indicated that they quickly understood the methodology used. On the other hand, 63% of the students needed help eliminating the strategies mastered in the game. Regarding the ludic part of the activity, 75% of the respondents indicated that they found it exciting and that it kept them attentive, while 61% considered that the way to get to the answer was simple. In analyzing the comments recorded, it was observed that the participants found the proposed matrix exciting and entertaining. However, it was also mentioned that some found it confusing or too difficult to understand.
Notably, 86% of the respondents indicated that the ludic activity awakened their interest in game theory. In comparison, 81% agreed with carrying out the activity at least once a semester. Finally, a second comment analysis process was conducted, where it was found that most users described it as interesting, educational, and an excellent way to understand payoff matrices in game theory. However, some aspects that could be improved in explaining the activity were also identified.
CONCLUSIONS
The findings derived from the prototype validation process indicate that the integration of a gamified activity captured greater student interest than lectures and fostered participation and application of prior knowledge. Although the gamified activity required an active implementation of disciplinary knowledge, the introductory activity provided a solid foundation, facilitating a gamified game experience with a delineated cognitive purpose.
Students showed a predilection for an educational approach that amalgamates playful exercises and lectures, evidencing improved cognitive indicators and a more fluid conceptual association when playful activities were used. This methodological binomial allowed a more efficient absorption and application of the critical concepts of game theory, highlighting the importance of diversified pedagogical strategies in the contemporary educational environment.
Nevertheless, areas for enrichment and optimization of the game approach were recognized. Among these, the need to provide more precise and concise explanations and integrate a wider variety of payoff matrices to broaden the exploration of strategies and avoid premature identification of Nash equilibrium by students stands out. This reflection prompts consideration of an iterative design for play activities in the future, where student feedback and experiences inform ongoing adaptations and refinements, thus ensuring the relevance and pedagogical effectiveness of the implemented activities.
REFERENCES
Ahmad, F., Almarri, O., Shah, Z. y Al-Fagih, L. (2023). Game theory applications in traffic management: A review of authority-based travel modelling. Travel Behaviour and Society, 32, 100585. https://doi.org/10.1016/j.tbs.2023.100585
Ahmad, F., Shah, Z. y Al-Fagih, L. (2023). Applications of evolutionary game theory in urban road transport network: A state of the art review. Sustainable Cities and Society, 98, 104791. https://doi.org/10.1016/j.scs.2023.104791
Amorós, P. (2022). Implementation in dominant strategies of quota rules to choose one candidate. Economics Letters, 216, 110557. https://doi.org/10.1016/j.econlet.2022.110557
Bartle, R. (1996). Hearts, clubs, diamonds, spades: Players who suit MUDs. Journal of MUD research, 1(1), 19.
Bonsón, E., Bednárová, M. y Perea, D. (2023). Disclosures about algorithmic decision making in the corporate reports of Western European companies. International Journal of Accounting Information Systems, 48, 100596. https://doi.org/10.1016/j.accinf.2022.100596
Cechella, F., Abbad, G. y Wagner, R. (2021). Leveraging learning with gamification: An experimental case study with bank managers. Computers in Human Behavior Reports, 3, 100044. https://doi.org/10.1016/j.chbr.2020.100044
Cullen, A., Alpcan, T. y Kalloniatis, A. (2022). Adversarial decisions on complex dynamical systems using game theory. Physica A: Statistical Mechanics and its Applications, 594, 126998. https://doi.org/10.1016/j.physa.2022.126998
Deterding, S., Dixon, D., Khaled, R. y Nacke, L. (2011). From Game Design Elements to Gamefulness: Defining “Gamification”. Proceedings of the 15th International Academic MindTrek Conference: Envisioning Future Media Environments, Tampere, Finland. https://doi.org/10.1145/2181037.2181040
Do, J. (2022). Cheating and compensation in price-fixing cartels. Journal of Economic Theory, 200, 105382. https://doi.org/10.1016/j.jet.2021.105382
Hafezalkotob, A., Nersesian, L. y Fardi, K. (2023). A policy-making model for evolutionary SME behavior during a pandemic recession supported on game theory approach. Computers & Industrial Engineering, 177, 108975. https://doi.org/10.1016/j.cie.2022.108975
Hallinger, P. y Wang, R. (2020). Analyzing the intellectual structure of research on simulation-based learning in management education, 1960–2019: A bibliometric review. The International Journal of Management Education, 18(3), 100418. https://doi.org/10.1016/j.ijme.2020.100418
Hou, F., Zhai, Y. y You, X. (2020). An equilibrium in group decision and its association with the Nash equilibrium in game theory. Computers & Industrial Engineering, 139, 106138. https://doi.org/10.1016/j.cie.2019.106138
Jain, L., Katarya, R. y Sachdeva, S. (2020). Recognition of opinion leaders coalitions in online social network using game theory. Knowledge-Based Systems, 203, 106158. https://doi.org/10.1016/j.knosys.2020.106158
Liu, Y. (2021). E-commerce Price War Based on Game Theory. 2021 3rd International Conference on Economic Management and Cultural Industry (ICEMCI 2021), https://doi.org/10.2991/assehr.k.211209.533
Loertscher, S. y Marx, L. (2020). A dominant-strategy asset market mechanism. Games and Economic Behavior, 120, 1-15. https://doi.org/10.1016/j.geb.2019.12.001
Mehmanpazir, F., Khalili-Damghani, K. y Hafezalkotob, A. (2022). Dynamic strategic planning: A hybrid approach based on logarithmic regression, system dynamics, Game Theory and Fuzzy Inference System (Case study Steel Industry). Resources Policy, 77, 102769. https://doi.org/10.1016/j.resourpol.2022.102769
Mohamed, H., Mirakhor, A. y Erbaş, S. (2019). Chapter 3 - Game Theory and Human Behaviour. In H. Mohamed, A. Mirakhor, & S. N. Erbaş (Eds.), Belief and Rule Compliance (pp. 43-68). Academic Press. https://doi.org/10.1016/B978-0-12-813809-0.00003-5
Munhoz, C. (2020). Gamifying Portuguese Language Learning: A Case Study Examining a Quest-Based Website to Prompt Oral Production and Interaction in Learners of Portuguese L2. Revista Brasileira de Linguística Aplicada, 20, 733-760. https://doi.org/10.1590/1984-6398202016396
Murphy, M. (2016). Design Thinking. In Landscape Architecture Theory (pp. 263–277). Washington, DC: Island Press/Center for Resource Economics. https://doi.org/https://doi.org/10.5822/978-1-61091-751-3_10
Nash, J. y John, F. (1950). Equilibrium points in n-person games. Proceedings of the national academy of sciences, 36(1), 48-49. https://www.pnas.org/doi/full/10.1073/pnas.36.1.48
Ozkan-Canbolat, E., Beraha, A. y Bas, A. (2016). Application of Evolutionary Game Theory to Strategic Innovation. Procedia - Social and Behavioral Sciences, 235, 685-693. https://doi.org/10.1016/j.sbspro.2016.11.069
Palacio, L. y Cortés, A. (2020). Conflicto 2x2: una lección de teoría de juegos en el laboratorio”. Cuadernos Económicos ICE, 99, 171-190. http://doi.org/10.32796/cice.2020.99.7013
Reyes, Y., Cañizares, R., Vargas, K. y García, M. (2020). Estudio de los principales beneficios del uso de la Gamificación en las plataformas educativas. Serie Científica de la Universidad de las Ciencias Informáticas, 13(6), 158-178. https://dialnet.unirioja.es/servlet/articulo?codigo=8590288
Rzeczycki, A. (2022). Supply chain decision making with use of game theory. Procedia Computer Science, 207, 3988-3997. https://doi.org/10.1016/j.procs.2022.09.461
Sabino, C. (2014). El proceso de investigación. Editorial Episteme.
Seymour, A., Borggren, M. y Baker, R. (2023). Escape the Monotony: Gamification Enhances Nursing Education. Journal of Emergency Nursing. https://doi.org/10.1016/j.jen.2023.06.004
Shi, Z., Zhou, H., Laat, C. y Zhao, Z. (2022). A Bayesian game-enhanced auction model for federated cloud services using blockchain. Futur. Gener. Comput. Syst., 136, 49–66. http://doi.org/10.1016/j.future.2022.05.017
Suárez-López, M., Blanco-Marigorta, A. y Gutiérrez-Trashorras, A. (2023). Gamification in thermal engineering: Does it encourage motivation and learning? Education for Chemical Engineers, 45, 41-51. https://doi.org/10.1016/j.ece.2023.07.006
Sun, Z., Liu, Y., Wang, J., Yu, R. y Cao, D. (2021). Cross-layer tradeoff of QoS and security in Vehicular ad hoc Networks: A game theoretical approach. Computer Networks, 192, 108031. https://doi.org/10.1016/j.comnet.2021.108031
Tarifa, E., Argañaraz, J., Astorga, F., Martínez, J. y Erdmann, E. (2011). Teoría de juegos aplicada a las políticas públicas. Strateg. Manag. Bus. Rev., 2(1), 25–37. http://www.exeedu.com/publishing.cl/strategy_manag_bus_rev/2011/Vol2/3-SM08-11-full.pdf
Tasnim, S., Sarimuthu, C., Lan, B. y Tan, C. (2023). A game theory approach for OLTC voltage control operation in an active distribution network. Electric Power Systems Research, 214, 108861. https://doi.org/10.1016/j.epsr.2022.108861
Valle, G. (2019). “LOS DOMINADOS Y EL ARTE DE LA RESISTENCIA”. UNA RESEÑA DE JAMES C, SCOTT. Revista Chakiñan de Ciencias Sociales y Humanidades, (7), 94-103. https://doi.org/10.37135/chk.002.07.08
Vanda, S., Nikoo, M., Hashempour, P., Al-Wardy, M., Franklin, J., Šimůnek, J. y Gandomi, A. (2022). Reservoir operation under accidental MTBE pollution: A graph-based conflict resolution framework considering spatial-temporal-quantitative uncertainties. Journal of Hydrology, 605, 127313. https://doi.org/10.1016/j.jhydrol.2021.127313
Wang, J., Wang, D., Li, X. y Qiao, J. (2023). Dichotomy value iteration with parallel learning design towards discrete-time zero-sum games. Neural Networks, 167, 751-762. https://doi.org/10.1016/j.neunet.2023.09.009
Wu, D. y Lisser, A. (2022). Using CNN for solving two-player zero-sum games. Expert Systems with Applications, 204, 117545. https://doi.org/10.1016/j.eswa.2022.117545
Wu, D. y Lisser, A. (2023). Improved saddle point prediction in stochastic two-player zero-sum games with a deep learning approach. Engineering Applications of Artificial Intelligence, 126, 106664. https://doi.org/10.1016/j.engappai.2023.106664
Zeng, X., Gao, H., Chen, Z., Yang, D. y Song, D. (2023). Cooperative optimization of speed planning and energy management for hybrid electric vehicles based on Nash equilibrium. Journal of Power Sources, 571, 233070. https://doi.org/10.1016/j.jpowsour.2023.233070
FINANCING
No external financing.
DECLARATION OF CONFLICT OF INTEREST
None.
ACKNOWLEDGMENTS (ORIGINAL SPANISH VERSION)
Se agradece a la Universidad Industrial de Santander por todo el apoyo recibido para el desarrollo de la investigación; especialmente al programa de Ingeniería Industrial.
AUTHORSHIP CONTRIBUTION
Conceptualization: Carlos Felipe Ardila Otero, Lissette Vanessa Pérez Rueda.
Data curation: Carlos Felipe Ardila Otero, María Camila Ballesteros Peña.
Formal analysis: María Camila Ballesteros Peña, Martha L. Torres Barreto.
Research: Carlos Felipe Ardila Otero, Lissette Vanessa Pérez Rueda.
Methodology: Carlos Felipe Ardila Otero.
Validation: Lissette Vanessa Pérez Rueda, Martha L. Torres-Barreto.
Writing - original draft: Carlos Felipe Ardila Otero, Lissette Vanessa Pérez Rueda.
Writing - revision and editing: María Camila Ballesteros Peña, Martha L. Torres-Barreto.